Lógica Proposicional

Introducción

Como habíamos visto en la unidad anterior vamos a trabajar con un sistema lógico en particular. El sistema de la lógica proposicional.

Ya lo habíamos caracterizado también. El sistema consta de:

1. Variables proposicional, las cuales servirán para formalizar cada una de las proposiciones. Ejemplo: \(p, q, r, ...\)
2. Constantes o conectivas proposicionales: las cuales servirán para formalizar las particular que realizan uniones o modifican a las proposiciones. Estas eran:
   • La negación (\(\neg, \sim\)).
   • La conjunción (\(\land, \bullet\)).
   • La disyunción (\(\lor\)).
   • El condicional (\(\supset, \rightarrow\)).
   • El bicondicional (\(\equiv, \leftrightarrow\)).
3. Los símbolos auxiliares, los cuales sirven para delimitar el alcance de las conectivas. Entre ellos encontramos a los paréntesis (\(( \ )\)), los corchetes (\([ \ ]\)) y las llaves (\(\{ \ \}\)).

Estos son los elementos que necesitamos para la poder llevar a cabo la formalización.

Antes de poder llevar a ver cómo analizamos los razonamientos, es primordial tener conocimiento y entrenamiento en cómo formalizar las proposiciones. Recordemos que lo que se trata es de pasar de lo que decimos en lenguaje natural -en nuestro caso el castellano- a un lenguaje formalizado -en este caso la lógica proposicional-.

Recordemos la noción de proposición:

Un enunciado completo descriptivo con la capacidad de ser verdadero o falso.

Entonces cuando nos embarquemos en la tarea de formalizar proposiciones, tenemos que tener en cuenta su definición, puesto que en ella se encuentran las características que nos dirán cómo tenemos que formalizar.

Además es importante tener en cuenta también las apariciones de las partículas que hacen referencia a las conectivas lógicas. Así como los signos de puntuación nos indican donde empieza y termina una oración, o como tiene que ser el énfasis y las pausas de la misma, las conectivas también nos pueden indicar donde empieza y termina una proposición y cómo es que se unen unas con otras. ¹

Simbolización

Para poder pasar del lenguaje ordinario al lenguaje formal, es necesario tener un entrenamiento que sea capaz de adquirir las habilidades para identificar cada uno de los elementos formales en el lenguaje ordinario. Es decir, poder leer cualquier oración y poder indicar qué parte de la oración es una proposición, una conectiva lógica y donde poner los símbolos auxiliares para que la fórmula en lógica proposicional tenga el mismo sentido que en lenguaje ordinario.

Aquí vamos a colocar algunos ejemplos básicos para que puedan entender, y luego se irá acompleja cada vez más.

Sobre los ejercicios

En el sitio web se encuentran en una solapa separada todos los ejercicios de las unidades.

Ir al link

Primero que nada vamos a ver algunos ejemplos de simbolizaciones básicas:

Dadas los siguientes enunciados simbolice usando la el sistema de lógica proposicional:

1. Juan trabaja todos los días.
2. María y Diego están de vacaciones.
3. El agua hierve a una temperatura de 100°C al nivel del mar

Resolución:

1. En el primero vemos que solo tenemos una proposición debido a que el enunciado es completo y es un enunciado descriptivo por lo que simplemente lo simbolizamos: \[p\]
2. En el segundo caso vemos que tenemos dos sujetos: Maria y Diego. Por lo que tenemos que ver qué es lo que están haciendo cada uno de ello. María está de vacaciones. Diego está de vacaciones también. Si bien los dos se encuentran en el mismo estado, son dos sujetos distintos. Por lo que para la lógica proposicional son dos proposiciones distintas: \(p\) para Maria y \(q\) para Diego. Cuando analizamos un enunciado que, a primera vista, parece una sola proposición pero no lo es, la recomendación es armar un diccionario. Esto quiere decir indicar cual es la referencia de cada una de las proposiciones.

   • Para este ejercicio sería así: \[p: María\ está\ de\ vacaciones\]

     \[q: Diego\ está\ de\ vacaciones\]

     \[p \bullet q\]

   • Como pueden ver aquí hemos introducido una conectiva lógica, la conjunción entre las dos proposiciones. Así se realiza una unión entre las proposiciones.

3. En el tercer caso, por más que parezca un enunciado bastante largo y de cierta complejidad es solo una proposición.
   • Por lo que su simbolización es la siguiente: \[p\]

Como hemos dicho más arriba estos son algunos ejemplos básicos, pero ya nos llevan a que tengamos ciertas cuestiones a considerar. Estas van a estar marcadas en el apartado en los pro tips:

Pro tips

• Verificar si el enunciado que se desea formalizar es un enunciado descriptivo capaz de ser verdadero o falso.
• Siempre hacer diccionario a la hora de simbolizar. Ayuda a ordenar mejor las proposiciones y evitar confusiones.
• Ubicar las conectivas lógicas para encontrar donde puede haber más de una proposición.

Reglas de formación

Para poder realizar formalizaciones correctas todo sistema de lógica posee reglas que cumplen la función de indicar cuándo y cómo las fórmulas del sistema se encuentran bien formadas.

La sintáxis del lenguaje natural también hace esto, por ejemplo:

“Hoy vamos a tener clase de lógica” es una oración bien fórmulada. Todos la podemos entender.

“De Vamos a hoy” por ejemplo no se encuentra bien fórmulada, no puede entender lo que dice.

En este sentido en lógica proposicional, por ejemplo:

\[p \bullet q\] es una fórmula bien formada (fbf) mientras que \[\bullet q p\] no lo es.

Las reglas de formación de la lógica proposicional son las siguientes:

1. Si \(\alpha\) ² es una fbf, entonces \(\sim \alpha\) también es una fbf.
2. Si \(\alpha\) y \(\beta\) es una fbf, entonces \(\alpha \lor \beta\) es una fbf.
3. No hay más fbf.

Como pueden ver las reglas de formación solo hacen uso de la negación y de la disyunción. Esto se debe a que todas las demás conectivas lógicas pueden definirse en base a la negación y disyunción. La negación y la disyunción son denominadas como terminos primitivos, es decir no se pueden definir por ninguna otra conectiva.

Por otro lado, la tercera regla indica una cancelación o clausura de todo tipo de regla de formación. Solo y solo esas reglas son las necesarias y suficientes para poder formalizar cualquier fórmula.

Como puede verse las reglas de formación también indican el orden en que las conectivas deben ser escritas. La negación va antes de cualquier proposición y las demás conectivas diádicas van entre dos proposiciones.

Mecanismos de decisión

Una vez que ya hemos realizado varios ejercicios de simbolización, podemos pasar al siguiente punto.

Como ya podemos formalizar los enunciados descriptivos, ahora nos queda por saber cuando dichas fórmulas son verdaderas y cuando falsas.

Para ello el sistema de lógica proposicional tiene sus mecanismos de decisión.

Noción de mecanismo de decisión

Un mecanismo de decisión es una serie de acciones determinadas y numeradas que permiten obtener algún beneficio. En estos casos es saber ciertas características de la verdad y falsedad de las proposiciones.

A tener en cuenta

Cuando veamos razonamientos también habrá otros mecanismos de decisión a considerar. Por ahora nos quedaremos con los mecanismos para las fórmulas propocisionales.

Los mecanismos de decisión pueden ser de distintos tipos:

• Sintácticos
• Semánticos:
  • Tabla de verdad
  • Reducción al absurdo

Además de que cada uno de ellos tiene una metodología distinta, la mayor diferencia que se encuentra entre ellos es que en los mecanismos de decisión semánticos hay una apelación a la noción de verdad que no se encuentra en los mecanismos de decisión sintácticos.

Sobre los mecanismos que veremos en el curso

Nosotros solo vamos a ver los mecanismos de decisión semánticos. Los mecanismos sintácticos los vamos a dejar para aquellos que quieran profundizar en el conocimiento lógico.

Como marcamos más arriba los mecanismos semánticos que veremos son dos: las tablas de verdad y la reducción al absurdo. La reducción al absurdo la veremos cuando veamos razonamientos.

Tabla de verdad

La tabla de verdad es un mecanismo de decisión que consta de realizar una tabla con todos los valores de verdad posible de la fórmula proposicional que deseamos analizar.

El propósito de la tabla de verdad es la de determinar si la fórmula proposicional es o bien tautológica, o bien contradictoria o una función de verdad o contingente. ¿Que quiere decir todo esto? Dependidendo del resultado de la tabla de verdad indicará distintas características de la fórmula:

• Si la fórmula es tautológica quiere decir que la matriz resultante de la tabla de verdad es siempre verdadera. Bajo cualquier valor de verdad de los componentes de la fórmula, esta siempre será verdadera.
• Si la fórmula es contradictoria quiere decir que la matriz resultante de la tabla de verdad es siempre falsa. Bajo cualquier valor de verdad de los componentes de la fórmula, esta siempre será falsa.
• Si la fórmula es contingente (o función de verdad) quiere decir que el valor de la matriz resultante va a depender del valor de los componentes. Puede que algunas veces sea verdadera y otra falsa.

¿Como hacer las tablas de verdad?

Para poder hacer las tablas de verdad vamos a realizar un procedimiento.

Atención

Tienen que aprender bien el procedimiento, una vez que lo hagan las suficientes veces se vuelve mecánico. Pero para que sea mecánico, deben practicar varias veces.

El procedimiento es el siguiente:

Dado cualquier formula proposcional siempre fijarse en la cantidad de proposiciones componentes de la fórmula. Por ejemplo si tenemos \(p \land q\) entonces serán dos proposisciones, si tenemos \(p\) será solo una y si tenemos \((p \lor q) \supset r\) serán tres.

Una vez que sabemos cuantas son debemos realizar tantas columnas haya de proposiciones atómicas. Para tomar un ejemplo vamos a tomar a \(p \land q\). Como tenemos dos escribiremos \(p\) en la primera fila y será nuestra primera columna, luego \(q\) y será nuestra segunda columna, a continuación vamos a escribir la fórmula proposicional: \(p \land q\).

Una vez terminado esto vamos a combinar todos los valores de verdad posibles que puede haber entre \(p\) y \(q\). Recordemos que la lógica proposicional es bivalente, es decir que solo tiene dos valores de verdad: verdadero (\(V\)) y falso (\(F\)). Entonces con \(V\) y con \(F\) tenemos que armar todas las posibilidades. Para ello vamos a recurrir a una pequeña fórmula matemática: \[2^n\] donde \(n\) es la cantidad de proposiciones atómicas que tiene la formula proposicional. En nuestro ejemplo tiene 2 (\(p\) y \(q\)) entonces tenemos que hacer \(2^2 = 4\) por lo que tendremos 4 posibilidades de mezclar los valores. Esto se traduce a que tenemos que hacer 4 filas para la tabla de verdad. Cada una de las filas es una posible interpretación de los valores de verdad.

Ahora para no olvidar ninguna combinación posible de valores, lo que vamos a hacer es tomar el resultado de la fórmula \(2^n\) y empezar a dividirlo en dos. Con nuestro ejemplo, tomamos el número \(4\) y lo dividimos en \(2\). El resultado es dos. Esto quiere decir que en la primera columna (\(p\)) de la tabla de verdad vamos a intercalar de a \(2\) los valores de verdad hasta agotar las líneas de interpretación. En la columna de \(p\) se intercalará 2 \(V\) y luego 2 \(F\). Luego al número que habíamos divido en 2 lo volvemos a dividir en 2, en nuestro ejemplo nos da 1. Es decir que vamos a intercalar 1 a 1 \(V\) y \(F\). Cuando llegamos a 1 no seguimos dividiendo. Ahí termina el procedimiento para determinar todos los posibles valores de verdad de las proposiciones atómicas de la tabla.

Una vez hecho eso la tabla nos quedará de esta manera:

Ahora lo que tenemos que hacer es poder indicar como son los valores de las conectivas de la fórmula proposicional. En nuetros ejemplo es solo la conjunción, a medida que se vaya complicando los ejericios serán más conectivas. Para ello tenemos que ver las tablas de verdad de cada una de las conectivas lógicas.

Tabla de verdad de la negación Extraida de (Zeballos y Cardozo 2019, 44)

Tabla de verdad de la conjunción. Extraidas de (Zeballos y Cardozo 2019, 44)

Tabla de verdad de la disyunción. Extraidas de (Zeballos y Cardozo 2019, 44)

Tablas de verdad del condicional. Extraidas de (Zeballos y Cardozo 2019, 44)

Tablas de verdad del bicondicional. Extraidas de (Zeballos y Cardozo 2019, 45)

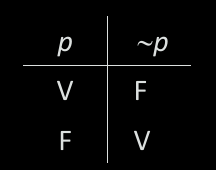
En el ejemplo que estamos trabajando el la misma tabla de verdad que la conjunción. Como pueden ver la conjunción se comporta de una determinada manera: solo es verdadera cuando ambos coyuntos (ambas proposiciones componentes) son verdaderas. En los demás casos es falsa. Pensemos que es lo que significa una conjunción. Dados dos hechos, estos se dan en conjunto, a la vez. Esto quiere decir que si uno de ellos no es verdadero, no puede ser que ambos se den a la vez.

Para las demas constantes lógicas recomendamos leer Zeballos y Cardozo (2019).

Con todo esto ahora podemos ver como quería nuestra tabla de verdad de ejemplo:

Una vez completada nuestra tabla podemos ver qué es la fórmula (una tautología, una contradicción o una función de verdad o contingente). En este caso si nos fijamos en la matriz resultante (la conectiva de mayor alcance) es contingente, puesto que tenemos valores de verdad y falsedad. No hay un solo valor de verdad, sino que nos aparecen los dos valores. Por lo que en la mayoría de los casos la conjunción será falsa, pero cuando ambos coyuntos sean verdaderos, será verdadera.

Para poder terminar el mecanismo se debe señalar la matriz resultante (en este caso vamos a colorear la matriz, lo ideal es encerrar con otro color la columna de la matriz) y luego abajo colocar (dado el caso):

• Fórmula tautológica
• Fórmula contradictoria
• Fórmula contingente

Ahora es momento de ejercitarse con las tablas de verdad: pueden hacer click en el siguiente aquí para ir a los ejercicios.

Presentación de clase

Notas

1. Incluso algunos lógicos las consideran como signos de puntuación. Es decir, van más allá de la analogía aquí propuesta. Esto es un tema de filosofía de la lógica, no es necesario indagar esto en un curso introductorio de lógico como el presente.

2. Utilizamos \(\alpha\) y \(\beta\) para varible meta-logicas. Estas variables comprenden desde una simple proposición cualquiera como \(p\) hasta propociones de cualquier complejidad como por ejemplo \((p \lor t) \supset [q \supset (r \bullet s)]\)