Silogismo aristotélico
Introducción
En un sentido amplio el Silogismo es definido por Aristóteles:
“Un Silogismo es un argumento en el cual, establecidas ciertas cosas, resulta necesariamente de ellas, por ser lo que son, otra cosa distinta de las antes establecidas”
En sentido estricto el silogismo es un razonamiento deductivo que consta de dos premisas y una conclusión. A las premisas se las denomina como premisas mayor y premisa menor.
Las premisas y la conclusión de los silogismos tienen determinadas características. Las premisas son los denominados juicios categóricos aristotélicos que tienen una forma muy particular. Por otro lado, además de los silogismos de juicios categóricos hay otros dos tipos de silogismos: el silogismo hipotético y el silogismo disyuntivo. El primero se caracteriza por tener una disyunción entre sus premisas. El segundo por tener un condicional entre ellas.
Silogismo categórico
En esta unidad nos vamos a enfocar en el silogismo categórico. Este silogismo puede definirme como aquel silogismo que tiene tres proposiciones categóricas y se compone de tres términos, de modo tal que, dos de esos términos se relacionan entre sí gracias a un tercer término. De esta relación es que surge la conclusión del silogismo
Ejemplo:
Ningún heroe es cobarde
Algunos soldados son cobardes
Algunos soldados no son heroes
Como puede observarse hay tres términos:
- Término mayor: Heroe
- Termino menor: Soldado
- Término medio: Cobarde
Como pueden observar el término mayor es el predicado de la conclusión (\(P\) de predicado), el término menor es el sujeto de la conclusión (\(S\) de sujeto) y el término medio (\(M\) de medio) no aparece en la conclusión es quien relaciona al termino mayor con el término menor.
Entonces si formalizamos el silogismo que tomamos como ejemplo nos queda:
Ningún \(P\) es \(M\)
Algún \(S\) es \(M\)
Algún \(S\) es \(P\)
Si observan bien el término mayor se encuentra en la premisa mayor, el término menor en la premisa menor. Solo se repite el término medio.
A su vez, el silogismo tiene un orden: premisa mayor, premisa menor y conclusión
Ahora bien, para poder realizar un mejor análisis de los silogismos y poder saber cuáles son válidos y cuáles son inválidos necesitamos saber su figura y su modo
Figura y modo
Figura del silogismo
La figura es la forma que tiene el silogismo y que se encuentra determinada por la posición del término medio en las premisas. Como son tres elementos de dos juicios categóricos hay 4 figuras posibles:
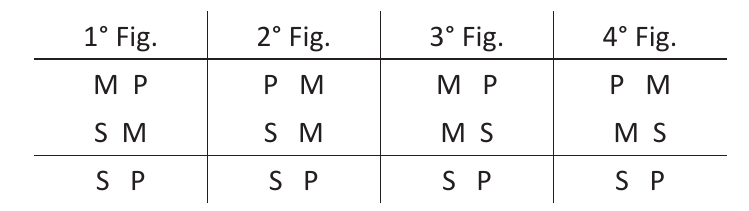
Ejemplos de las figuras
1° Figura:
Todas las sales de sodio son sustancias solubles en agua
Todos los jabones son sales de sodio
Todos los jabones son sustancias solubles en agua
2° Figura:
Todos los amigos de Paula son estudiosos
Ningún hermano de Daniel es estudioso
Ningún hermano de Daniel es amigo de Paula
3° Figura:
Todas las computadoras son importadas
Algunas computadoras son de mala calidad
Algunos objetos de mala calidad son importados
4° Figura:
Ningún Ministro es holgazán
Todo Holgazán es divertido
Algunas personas divertidas no son ministros
Modo del silogismo
El modo del silogismo hace referencia a la cantidad (si es una proposición universal o particular) y a la cualidad (si es afirmativa o negativa). De esta manera teniendo en consideración ambos aspectos los juicios categóricos son 4: Afirmativo universal (\(A\): Todo \(S\) es \(P\)); Negativo universal (\(E\): Ningún \(S\) es \(P\)); Afirmativo particular (\(I\): Algún \(S\) es \(P\)); Negativo particular (\(O\): Algún \(S\) no es \(P\)).
Si vamos a nuestro primer ejemplo, el de los heroes y soldados, su modo es \(EIO\).
Las distintas combinaciones de juicios categóricos nos dan 64, puesto que van desde \(AAA\) hasta \(OOO\). A su vez, esto hay que multiplicar por 4 ya que el orden de los términos varía según las figuras.
De esta manera llegamos a \(64 * 4 = 256\). Existen 256 posibles silogismos. No todos ellos son válidos. Para poder determinarlos los silogismos necesitan cumplir todas las reglas de la silogística para que sea válido.
Concluyendo esta sección, podemos decir que el silogismo está determinado por su figura y su modo.
Reglas de los silogismos
Estas reglas se dividen en dos grupos:
- Reglas de los términos
- Reglas de las proposiciones que lo componen
Reglas de los términos
Primera regla
TODO SILOGISMO DEBE TENER TRES TÉRMINOS: es decir Término Mayor (P) Término Menor (S) y Término Medio (M)
Un ejemplo que viola esta regla es el siguiente silogismo:
Toda llama quema
Algún animal es una llama
Algún animal quema
Segunda regla
NINGÚN TÉRMINO DEBE APARECER EN LA CONCLUSIÓN CON MAYOR EXTENSIÓN QUE EN LAS PREMISAS: para entender esta regla debemos recordar que un término está tomado en toda su extensión cuando es sujeto de una proposición universal o predicado de una proposición negativa.
Un ejemplo que viola esta regla es el siguiente silogismo:
Todo pez es vertebrado
Todo pez es un animal acuático
Todo animal acuático es vertebrado
Tercera regla
EL TÉRMINO MEDIO NO DEBE FIGURAR EN LA CONCLUSIÓN: Ésta regla se limita a poner en forma imperativa una condición necesaria para que pueda hablarse de silogismo
Cuarta regla
EL TÉRMINO MEDIO DEBE ESTAR TOMADO, AL MENOS UNA VEZ, EN TODA SU EXTENSIÓN: para entender esta regla también debemos recordar la extensión de los términos como lo hicimos en la regla número tres.
Un ejemplo que viola esta regla es el siguiente silogismo:
Todo loro es un animal
Todo perro es un animal
Todo perro es un loro
Reglas de las proposiciones
Quinta regla
DE DOS PREMISAS NEGATIVAS NO SE SIGUE CONCLUSIÓN
Un ejemplo que viola esta regla es el siguiente silogismo:
Ningún uruguayo es africano
Ningún africano es montevideano
Ningún montevideano es uruguayo
Sexta Regla
DE DOS PREMISAS AFIRMATIVAS NO SE SIGUE CONCLUSIÓN NEGATIVA: De dos afirmaciones no puede derivarse una negación.
Un ejemplo que viola esta regla es el siguiente silogismo:
Todo argentino es americano
Todo salteño es argentino
Algún salteño no es americano
Septima Regla
LA CONCLUSIÓN SIEMPRE SIGUE LA PARTE MÁS DEBIL: la particular respecto de la universal y la negativa respecto de la afirmativa. Si hay una premisa particular, la conclusión debe ser particular; si hay una premisa negativa, la conclusión debe ser negativa; si hay una premisa particular y negativa, o una premisa particular y otra negativa, en ambos casos, la conclusión debe ser particular y negativa.
Un ejemplo que viola esta regla es el siguiente silogismo:
Ningún amigo de Graciela es japonés
Todo filósofo es amigo de Graciela
Todo filósofo es japonés
Octava Regla
DE DOS PREMISAS PARTICULARES NO SE SIGUE CONCLUSIÓN
Un ejemplo que viola esta regla es el siguiente silogismo:
Algunos hombres son europeos
Algunos hombres son americanos
Algunos americanos son europeos
Con todo esto ya es posible determinar la validez de los silogismos. Por supuesto recordamos que es menester leer el capítulo del libro y realizar los ejercicios.